Taith Fawr i'r Ogofâu
Mae Siôn Corn yn paratoi at ei daith flynyddol i ogofâu ar draws y Canolbarth cyn y Nadolig. Bydd yn dechrau ac yn gorffen ei daith yn Aberystwyth, lle mae'r sled wedi'i llenwi ac mae'r ceirw yn ysu am gael cychwyn. Ei dasg? Ymweld â phob tref unwaith yn union, dosbarthu'r nwyddau Nadoligaidd, a dychwelyd i Aberystwyth cyn iddi nosi.
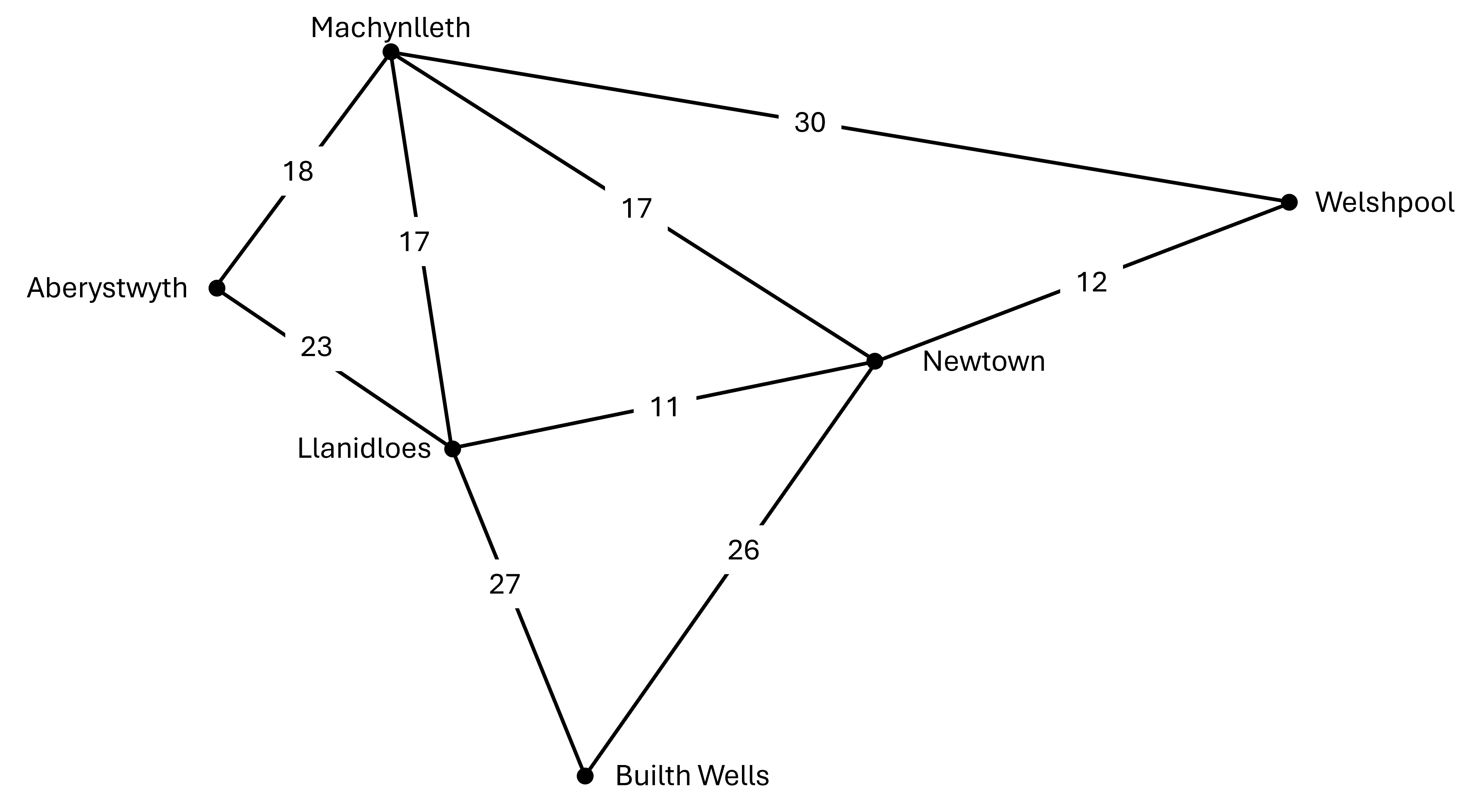
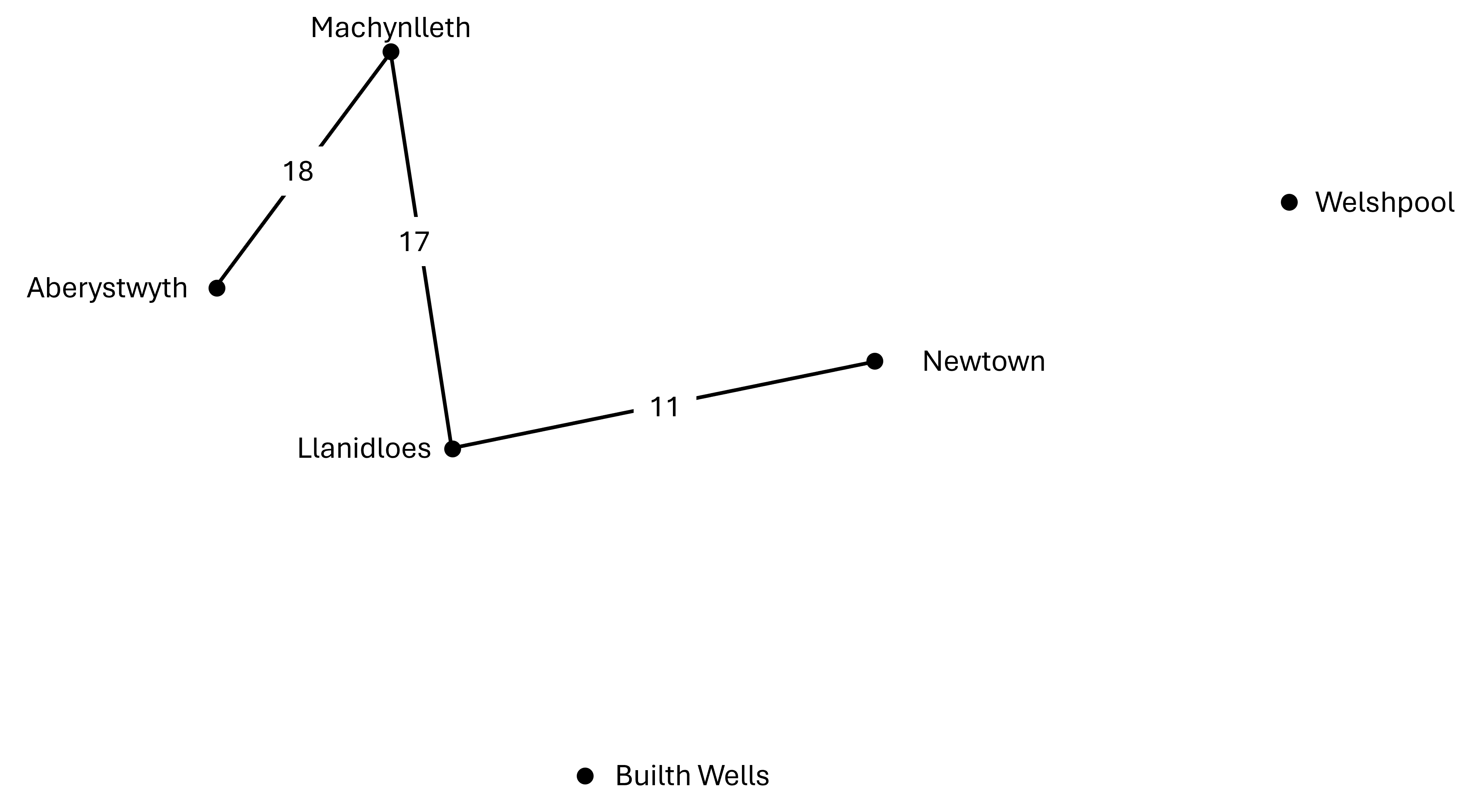
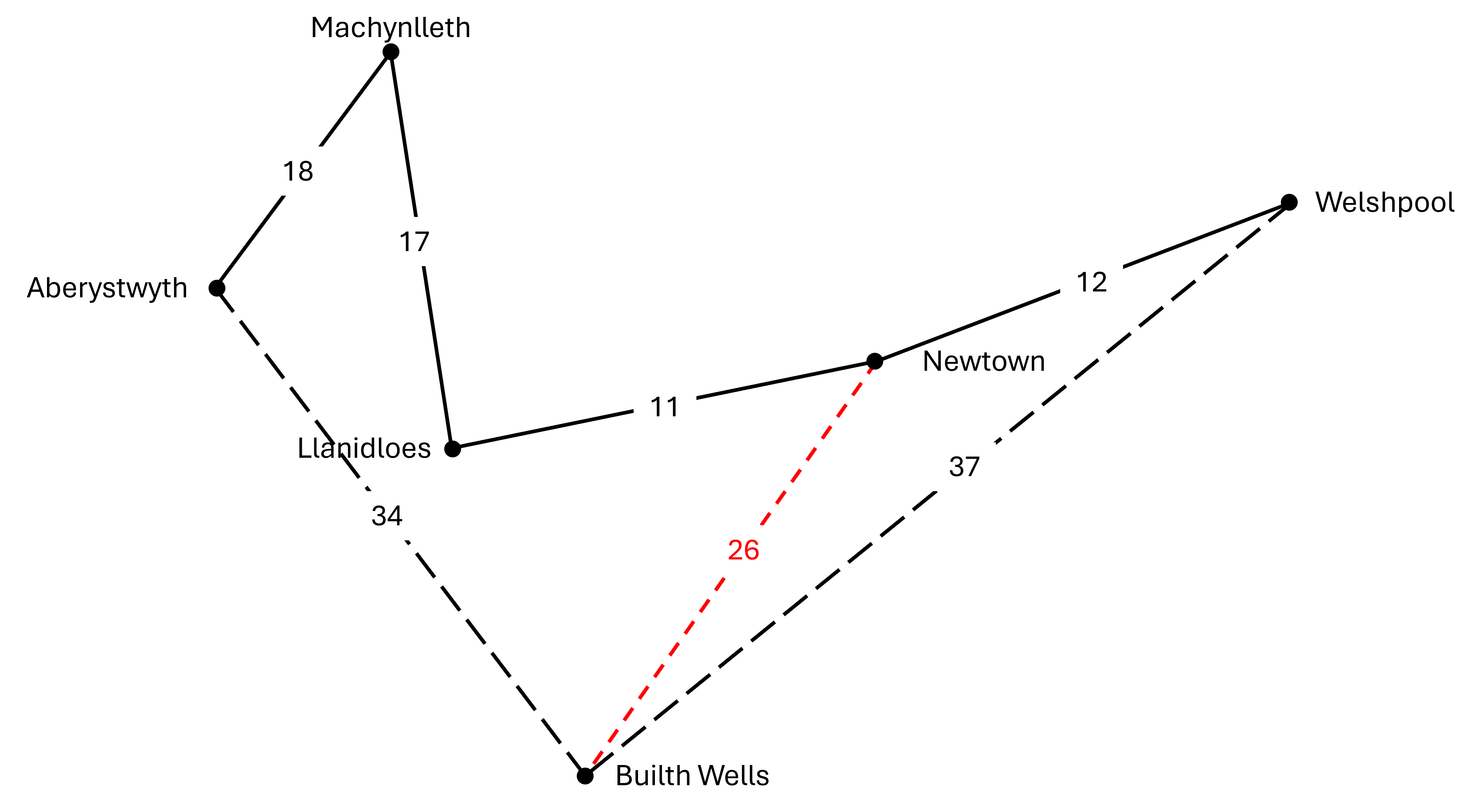
I helpu Siôn Corn i gynllunio ei daith i'r ogofâu, rydym wedi rhoi'r pellteroedd rhwng pob pâr o drefi mewn tabl cyfeirio defnyddiol. Mae rhai o'r llwybrau wedi'u dangos yn y map isod - ond mae'r rhwydwaith llawn yn cynnwys pob cysylltiad uniongyrchol posib, sy'n golygu y gall Siôn Corn ddewis y llwybr mwyaf effeithlon ar gyfer ei sled.
Y map anghyflawn:
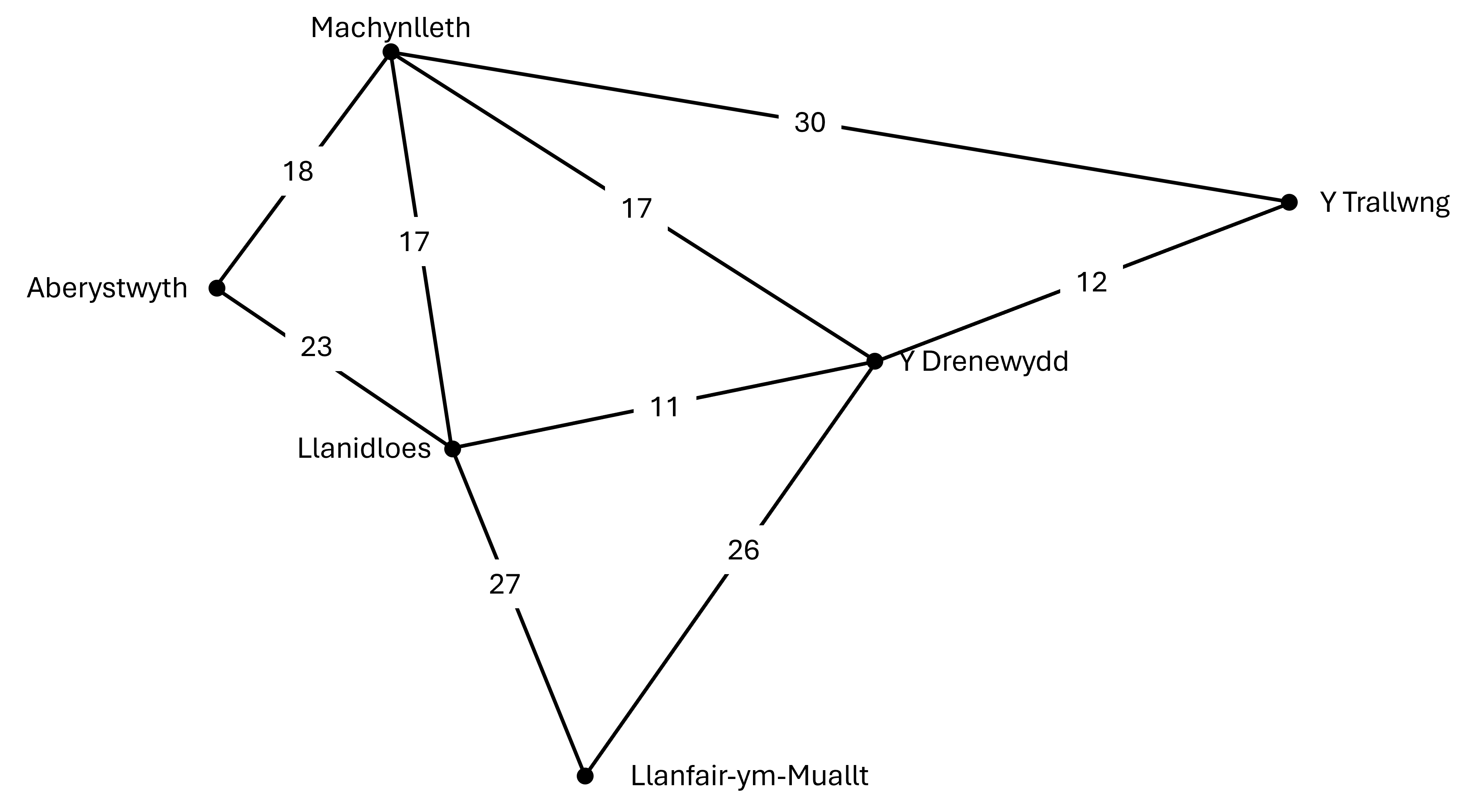
Y tabl cyfeirio:
| Aberystwyth | Llanfair-ym-Muallt | Llanidloes | Machynlleth | Y Drenewydd | Y Trallwng | |
|---|---|---|---|---|---|---|
| Aberystwyth | - | 34 | 23 | 18 | 29 | 43 |
| Llanfair-ym-Muallt | 34 | - | 27 | 36 | 26 | 37 |
| Llanidloes | 23 | 27 | - | 17 | 11 | 22 |
| Machynlleth | 18 | 36 | 17 | - | 17 | 30 |
| Y Drenewydd | 29 | 26 | 11 | 17 | - | 12 |
| Y Trallwng | 43 | 37 | 22 | 30 | 12 | - |
Sut i ddatrys yr her
Dyma enghraifft o Broblem y Trafaeliwr Gwerthu (neu Broblem y Gwerthwr Teithiol). Mae sawl ffordd wahanol o ddatrys y rhain. Bydd y rhan hon yn eich tywys trwy'r dull mathemategol y gwnaethom ni ei ddefnyddio.
Cam 1: Y map
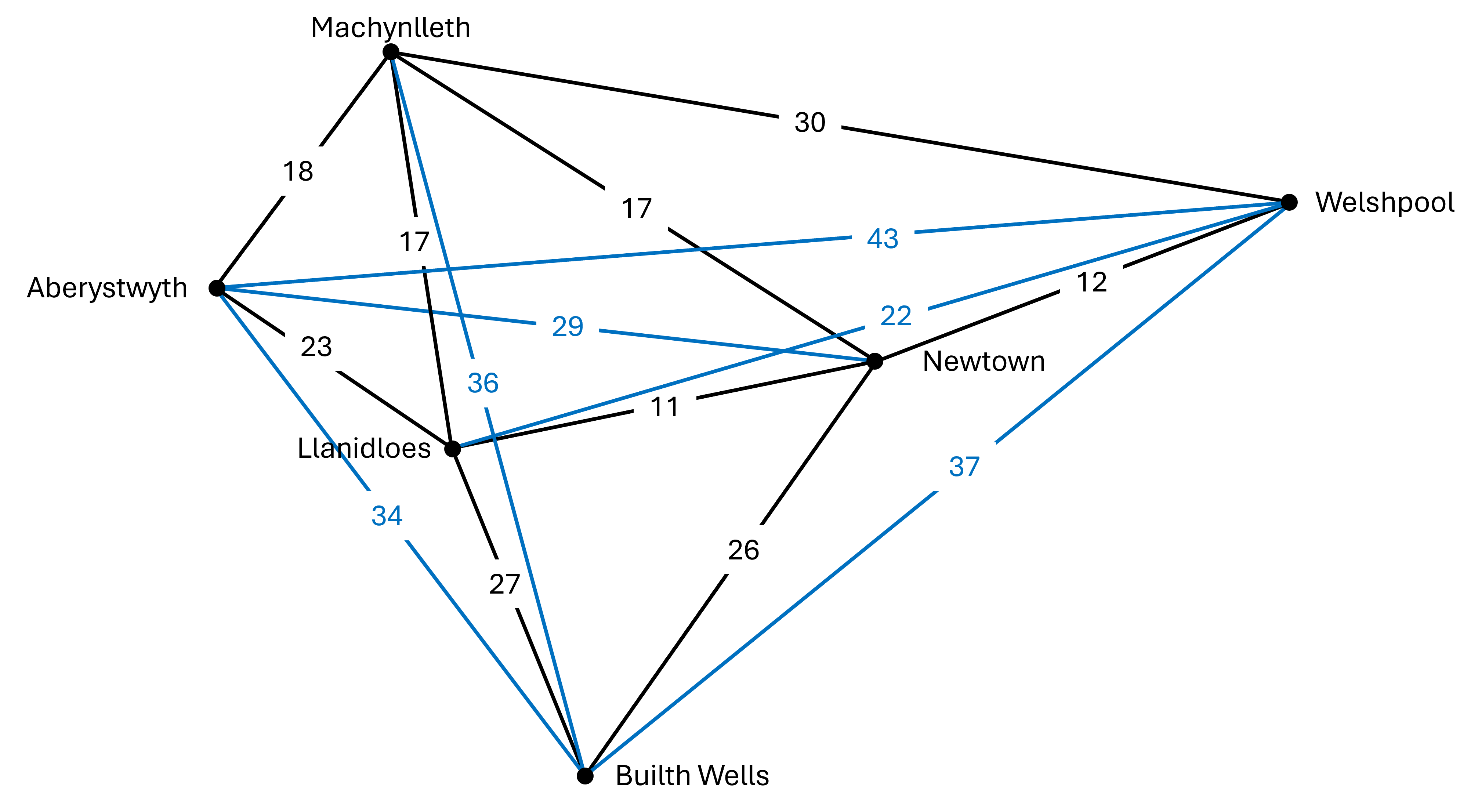
Fel y dywedwyd, mae'r map a roddir gyda'r pos hwn yn anghyflawn. Felly, efallai y bydd angen i chi ail-lunio'r map gyda'r holl gysylltiadau a mesuriadau i'ch helpu i weld y broblem hon.
Rydym wedi dangos y llinellau coll â lliw glas.
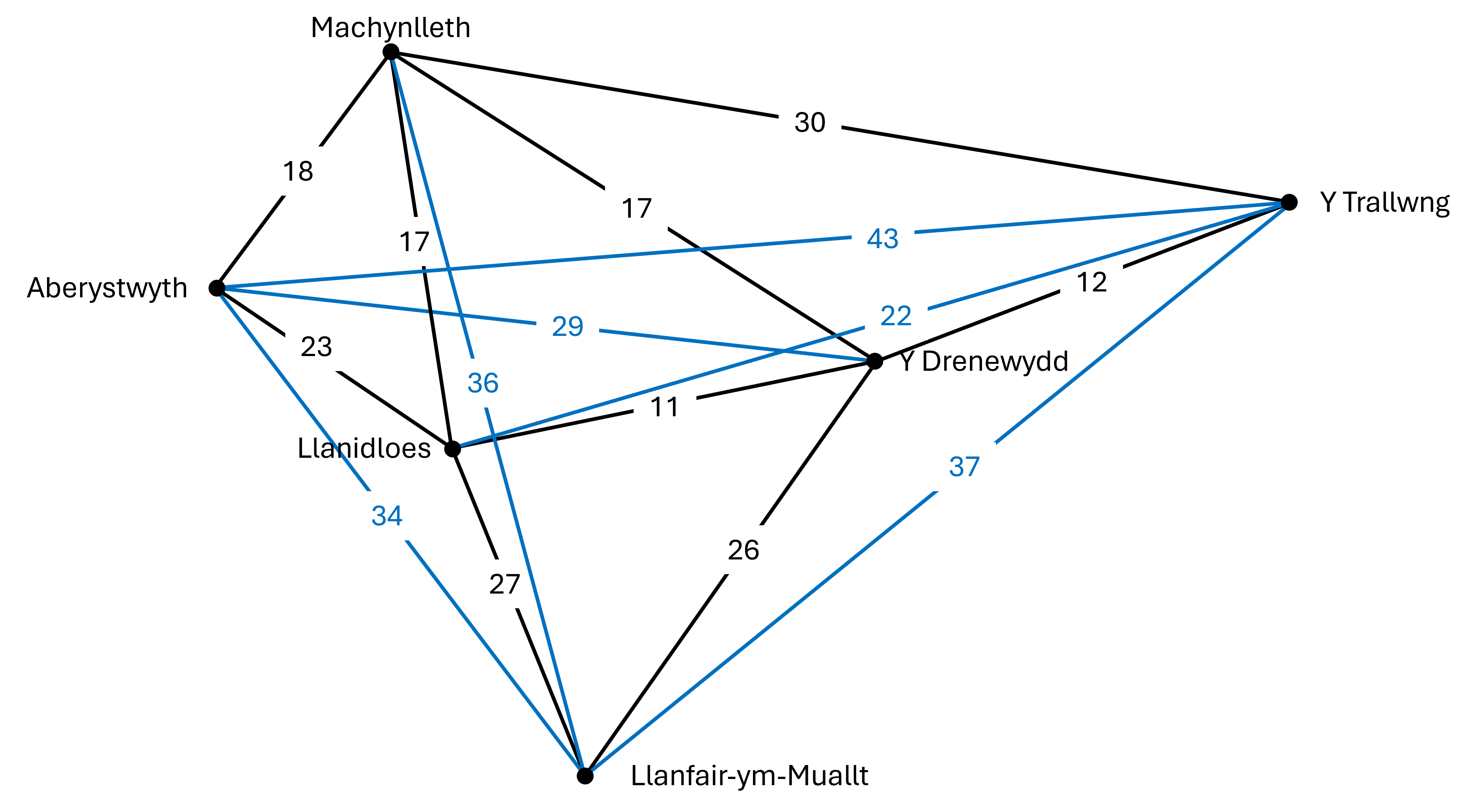
Cam 2: Coeden Rychwantu Leiaf (MST)
I'r broblem hon, fe ddewisasom ni lunio rhywbeth o'r enw Coeden Rychwantu Leiaf, a ddatblygwyd gan ddefnyddio dull o'r enw Algorithm Prim. Mae hyn yn cysylltu'r holl leoedd â'i gilydd gan ddefnyddio'r llwybrau byrraf posib. Gadewch i mi fynd â chi trwy sut mae hyn yn gweithio.
-
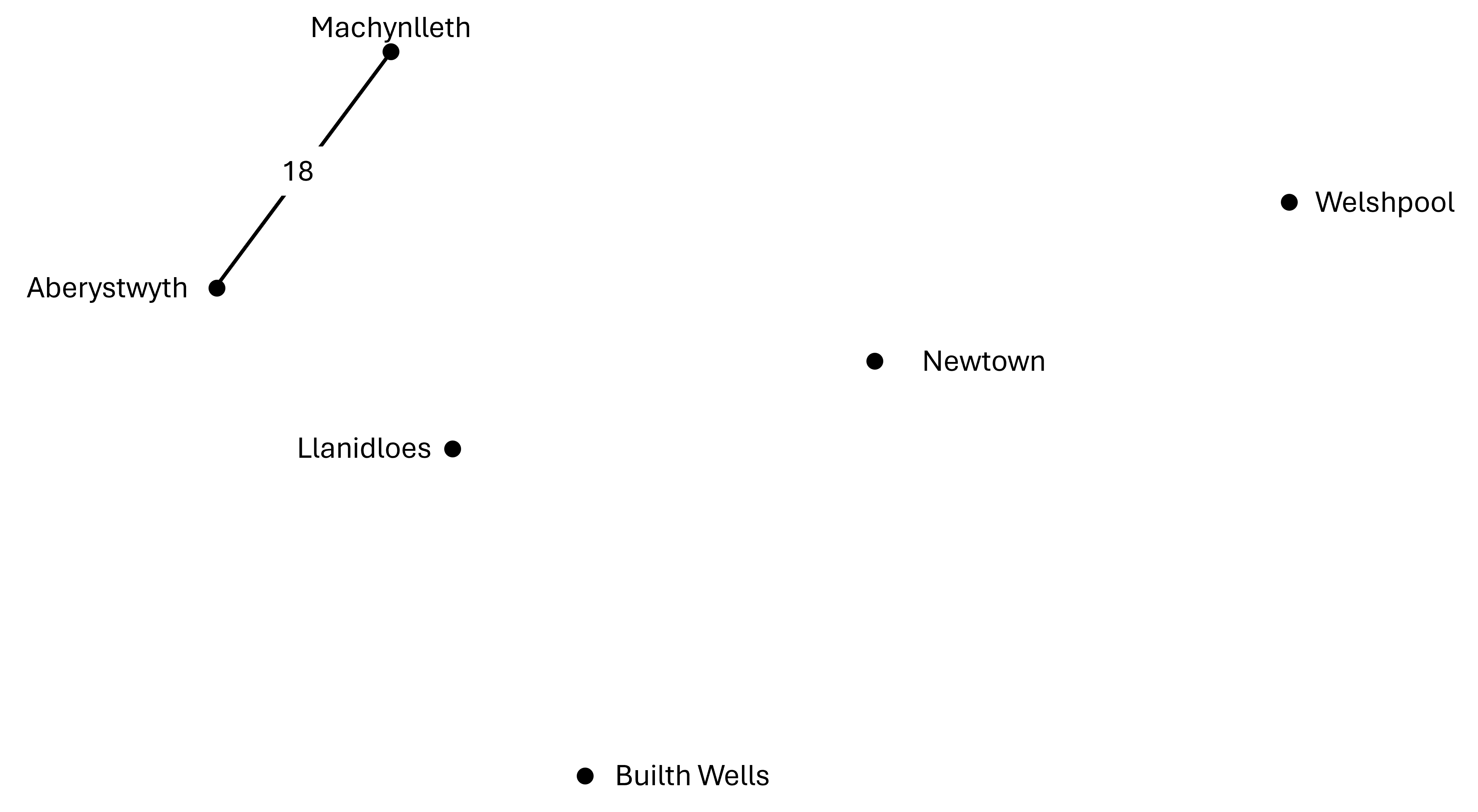
Edrychwch ar Aberystwyth a nodi'r llwybr byrraf sy'n arwain i ffwrdd ohoni.
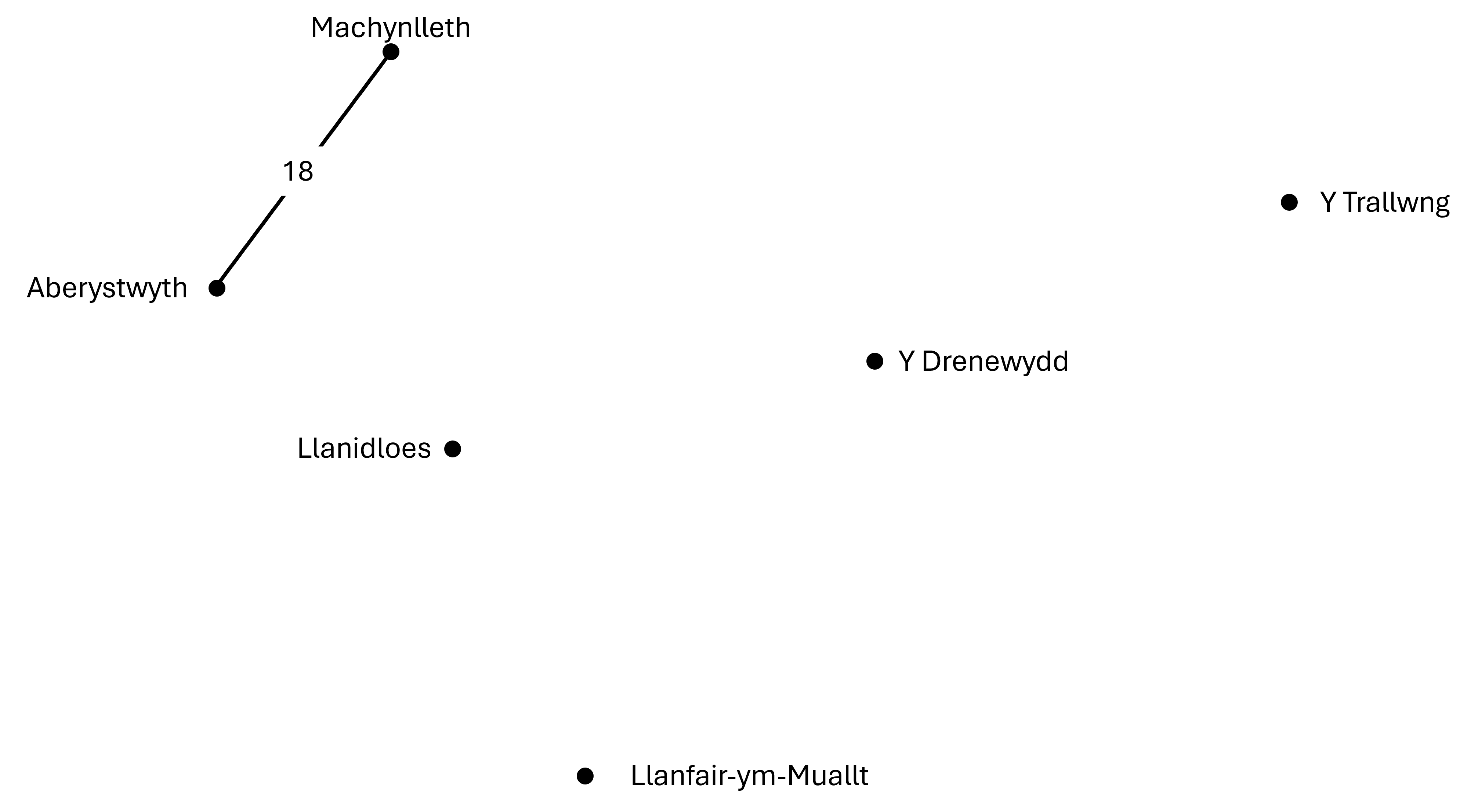
-
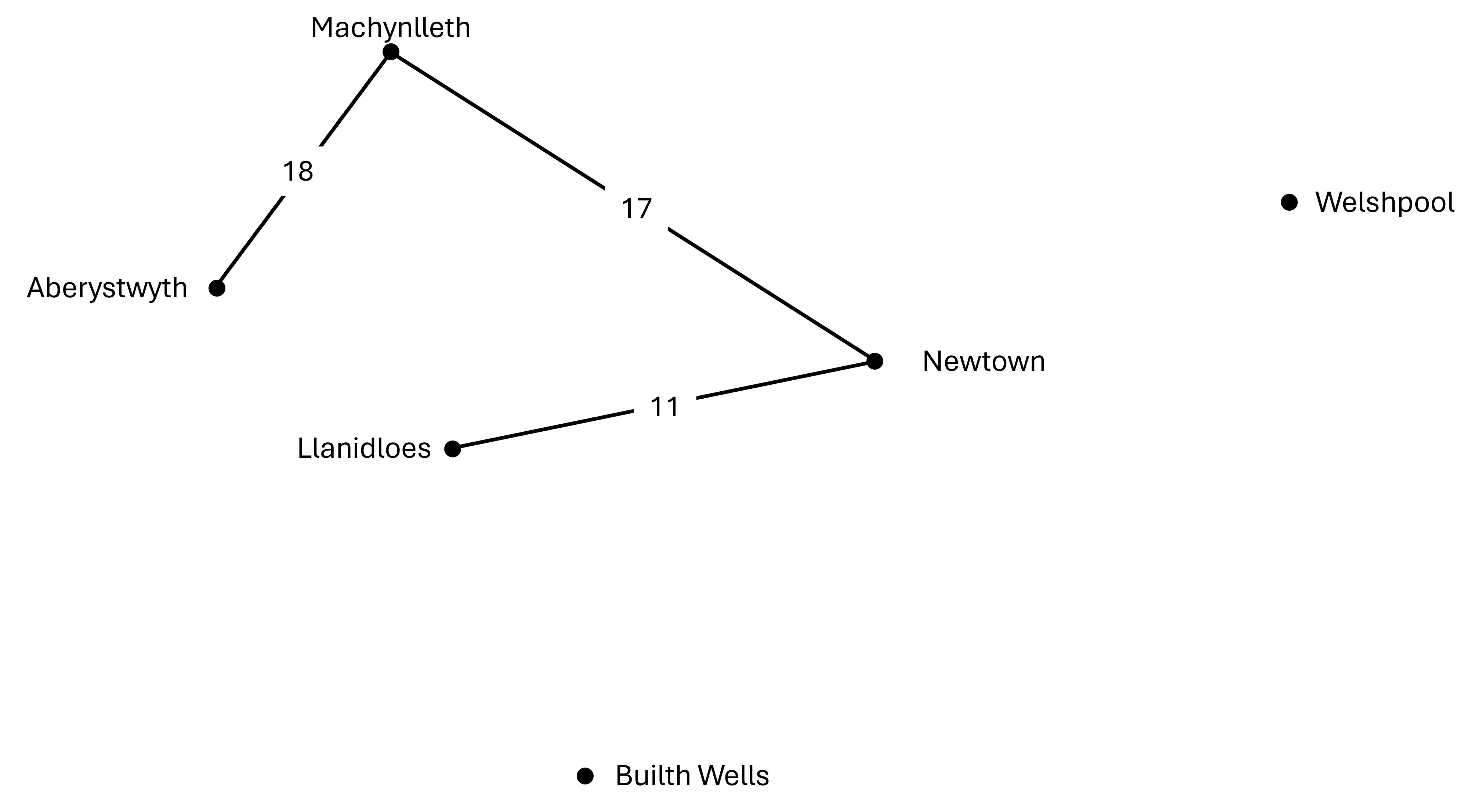
Nawr mae angen dod o hyd i'r llwybr byrraf i ffwrdd o'r naill neu'r llall o'r nodau cysylltiedig hyn. Ond arhoswch - mae dau opsiwn! Mae hyn yn golygu y bydd angen i ni greu ail goeden rychwantu fel y gallwn ddilyn y ddau bosibilrwydd.
Llwybr 1:

Llwybr 2:

-
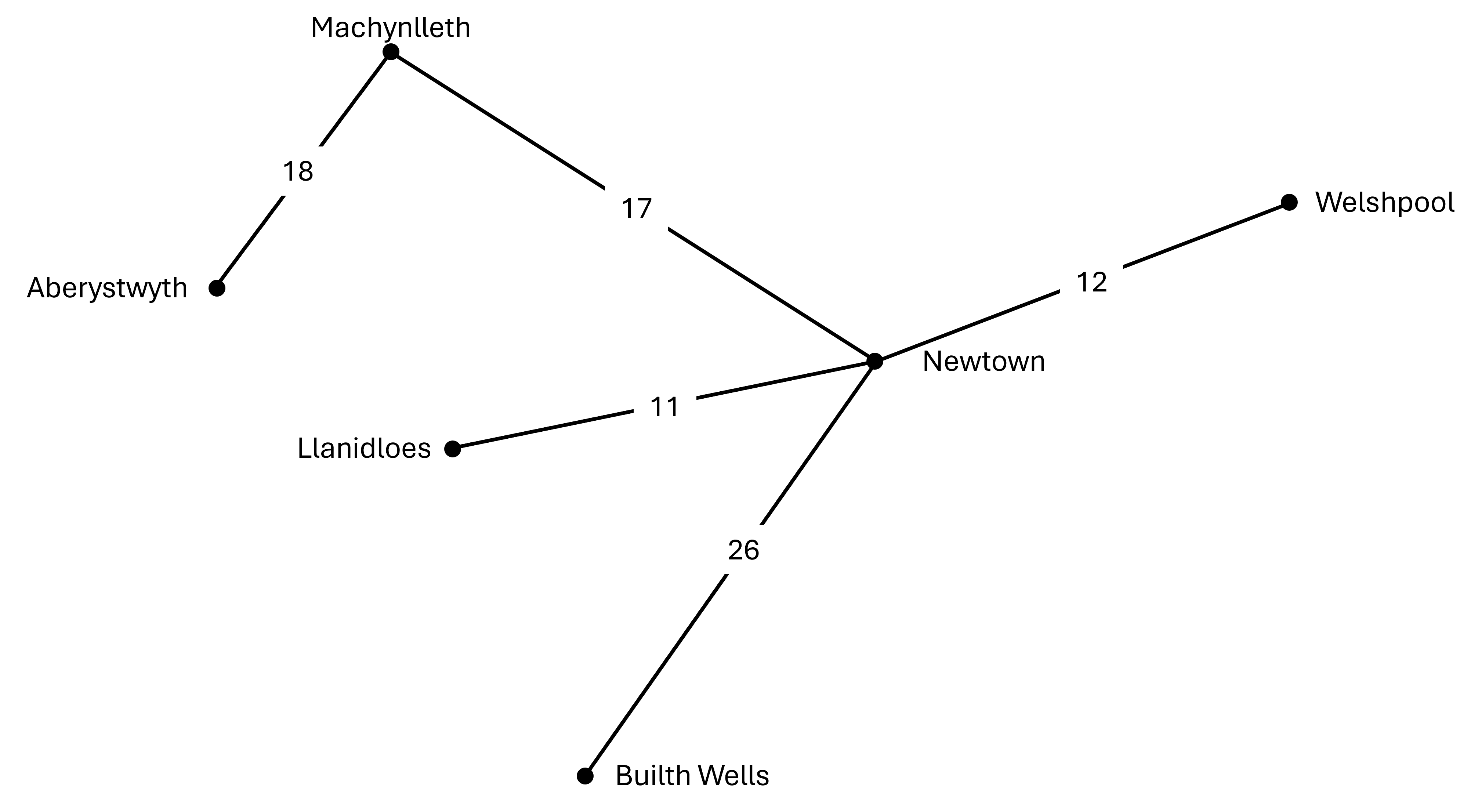
Y cam nesaf yw ystyried p'un yw'r llwybr byrraf sydd ar gael i gysylltu tref arall â'n rhwydwaith. Bob tro rydyn ni'n gwneud hyn rydym ni'n cysylltu trefi newydd â'n rhwydwaith.
Llwybr 1:
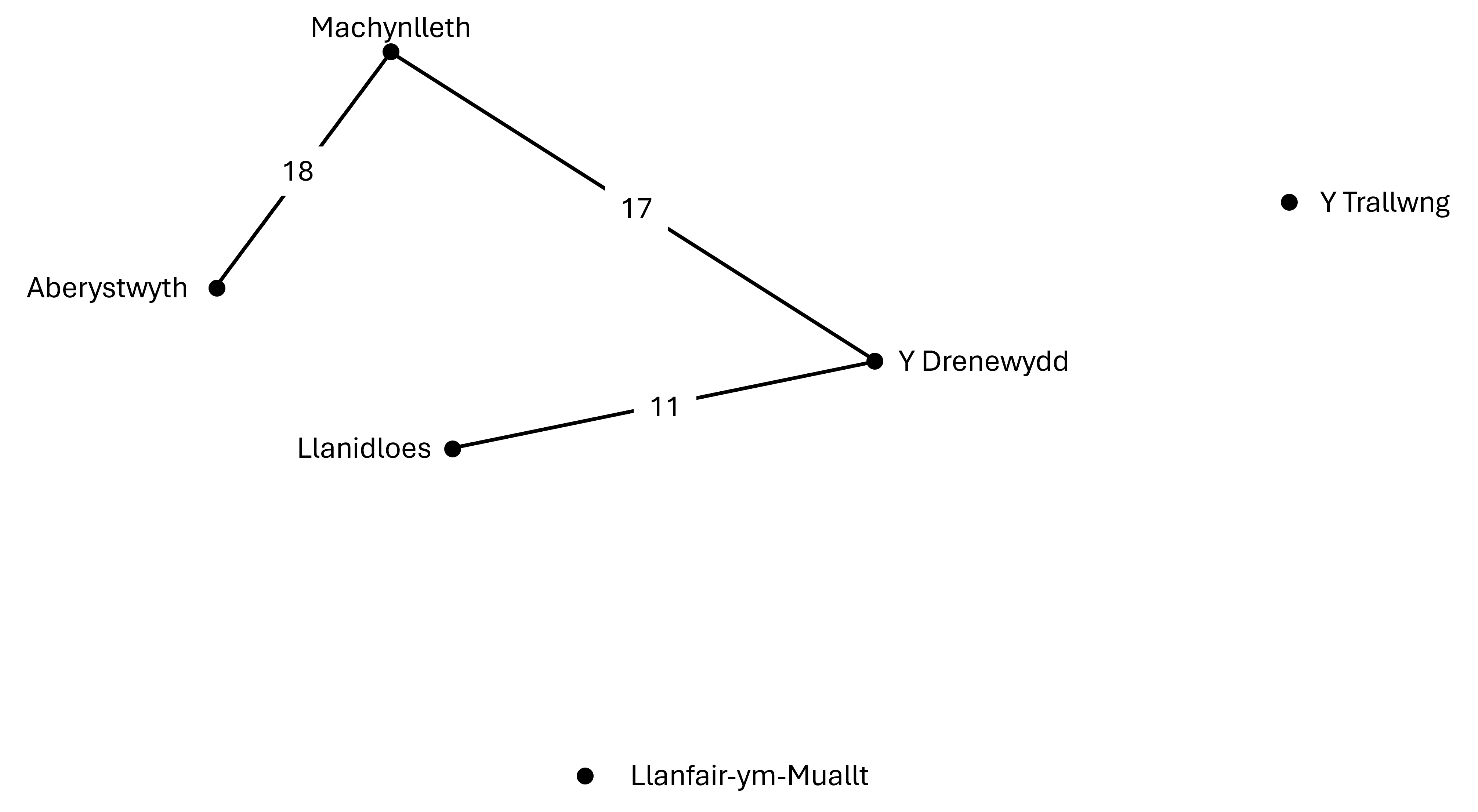
Llwybr 2:
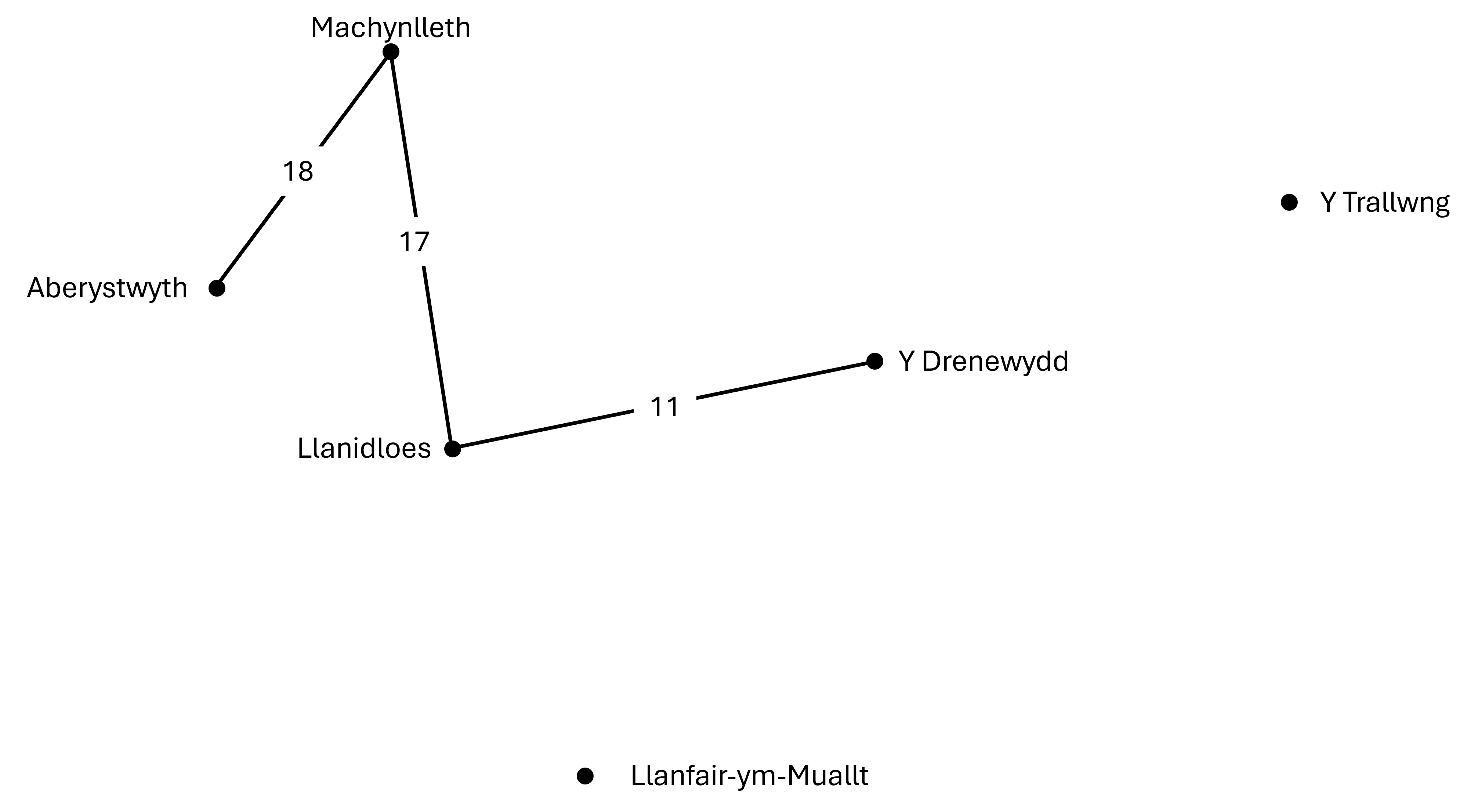
-
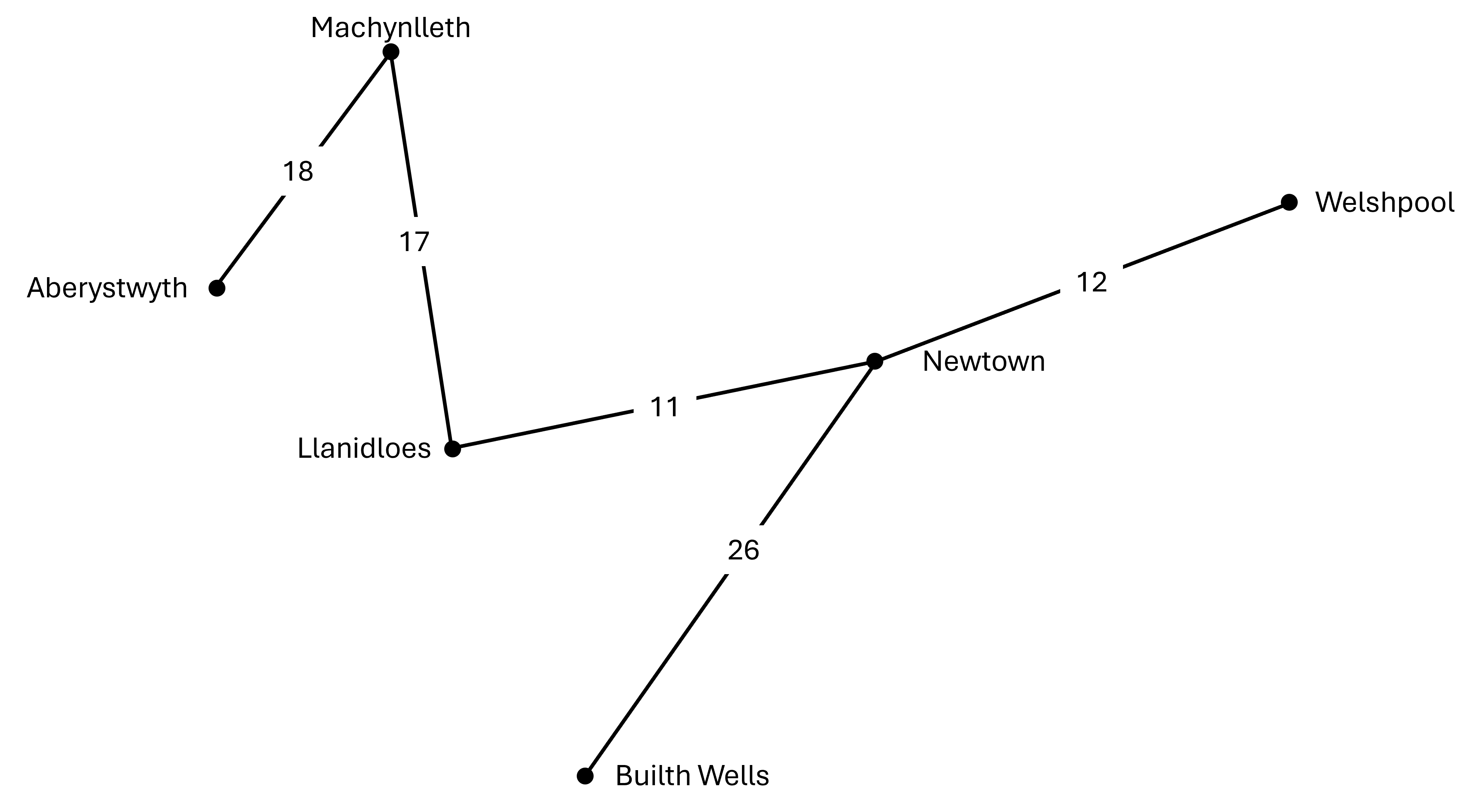
Ailadroddwch y cam blaenorol i ychwanegu'r trefi olaf at ein rhwydwaith.
Llwybr 1:
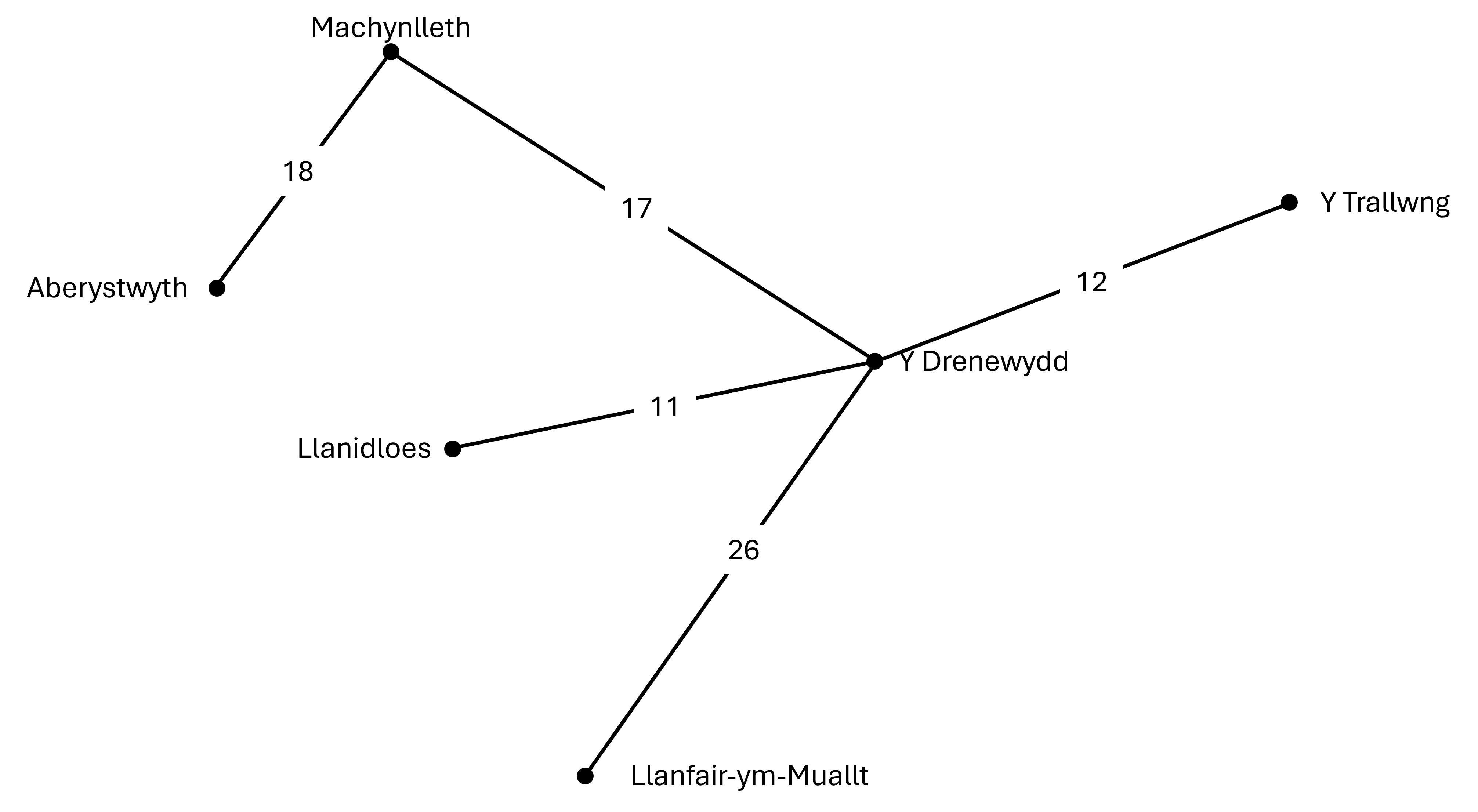
Llwybr 2:
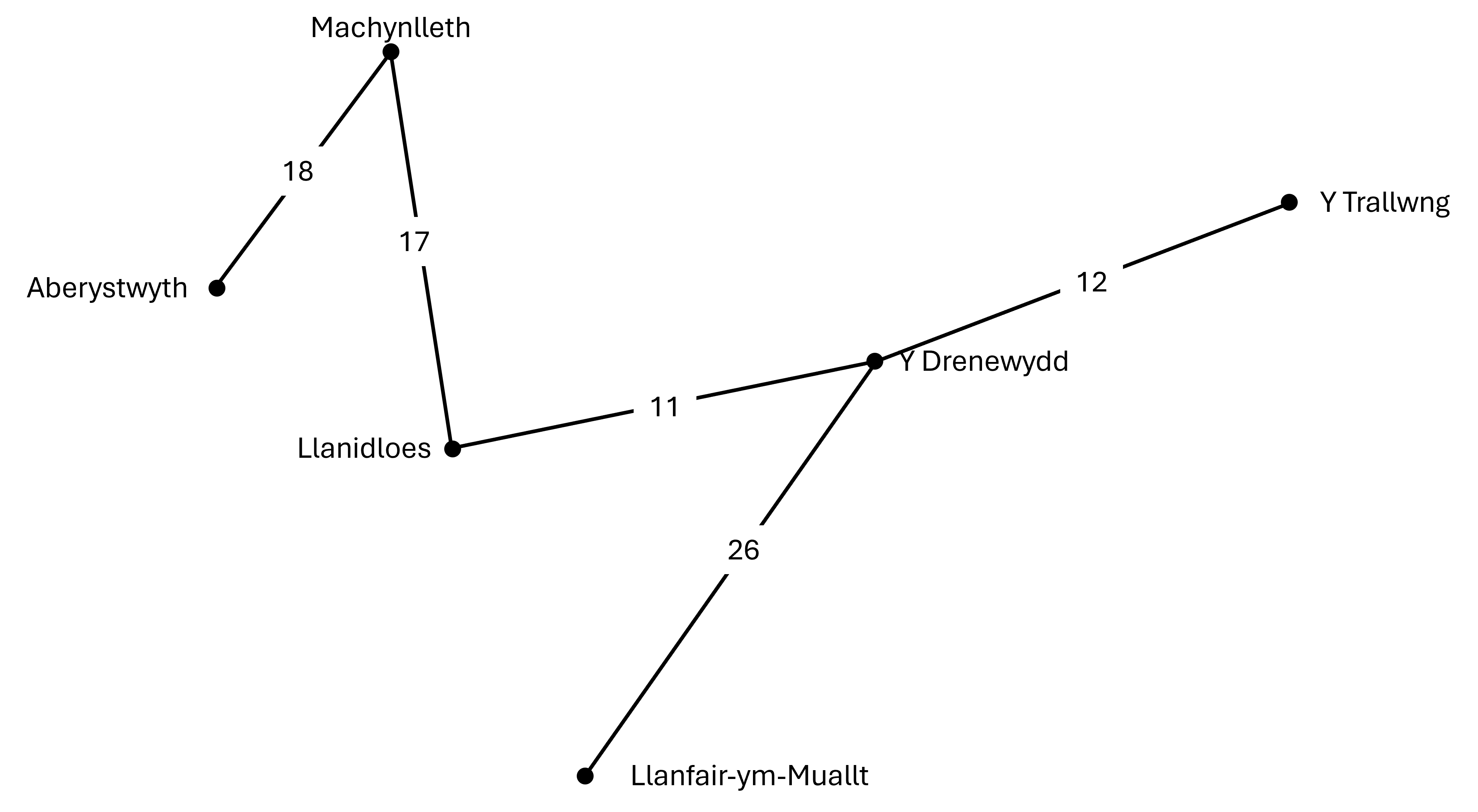
Cam 3: Ffurfio'r ddolen
Erbyn hyn mae gennym ni ddwy Goeden Rychwantu Leiaf sy'n cysylltu ein trefi â'i gilydd drwy'r llwybrau byrraf. Serch hynny, nid yw'r llwybrau hyn yn addas ar gyfer ein her ni, oherwydd er mwyn teithio i bob lle ac yn ôl i Aberystwyth, fe fyddai'n rhaid i Siôn Corn fynd drwy rai mannau fwy nag unwaith.
Felly, mae angen i ni ystyried sut i roi'r llwybr ar ffurf dolen.
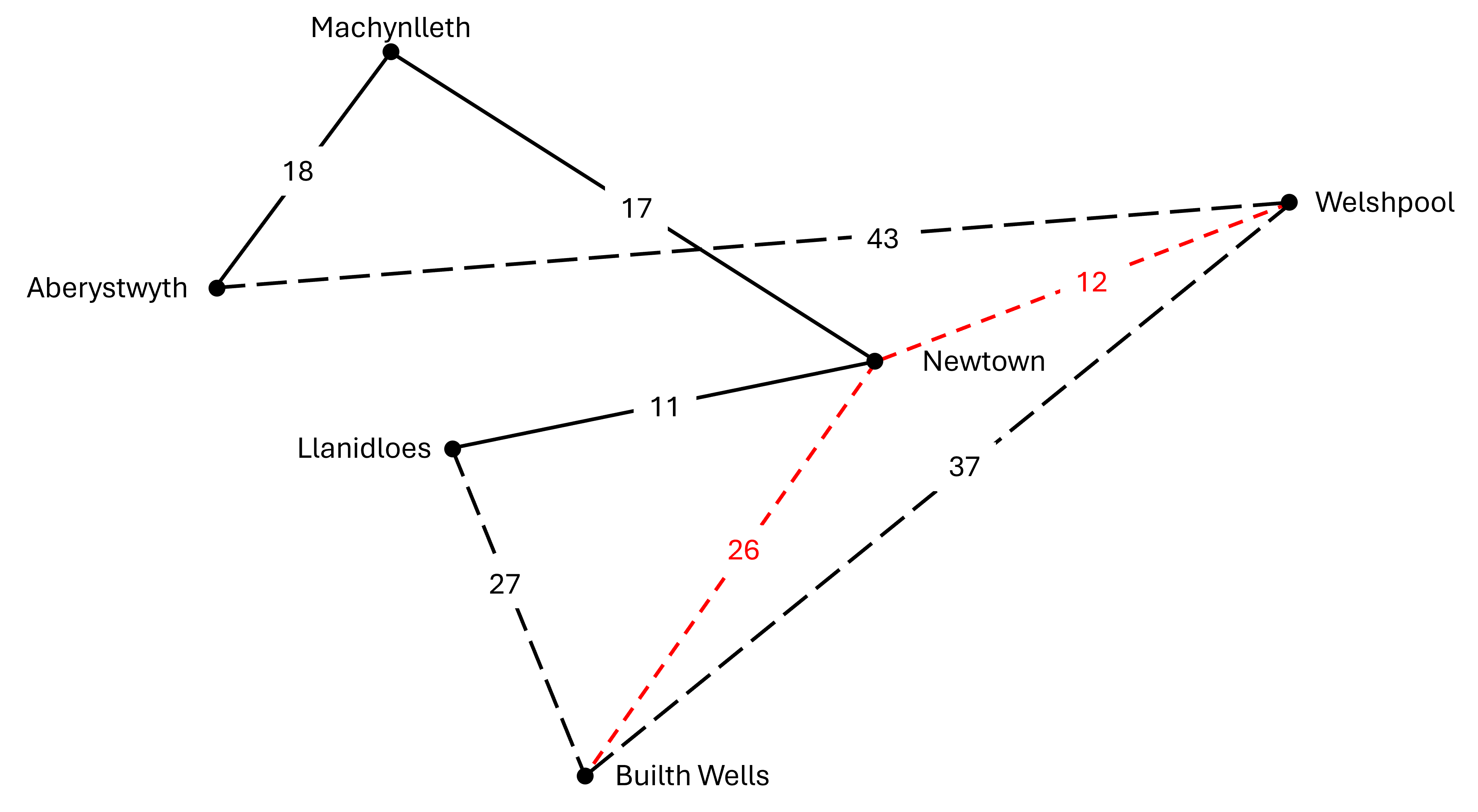
I wneud hyn, gadewch i ni edrych ar ein llwybrau. Yn y ddau achos mae ein llwybr yn ymrannu yn y Drenewydd. Mae angen i ni edrych ar sut y gallwn gael gwared ar yr un hiraf o'r rhain a rhoi, yn ei le, ddolen sy'n cysylltu yn ôl ag Aberystwyth.
Yn y mapiau isod mae'r ychwanegiadau newydd wedi'u marcio â llinellau doredig du, a'r llwybrau sydd wedi'u dileu wedi'u dangos â llinellau coch.
Llwybr 1:
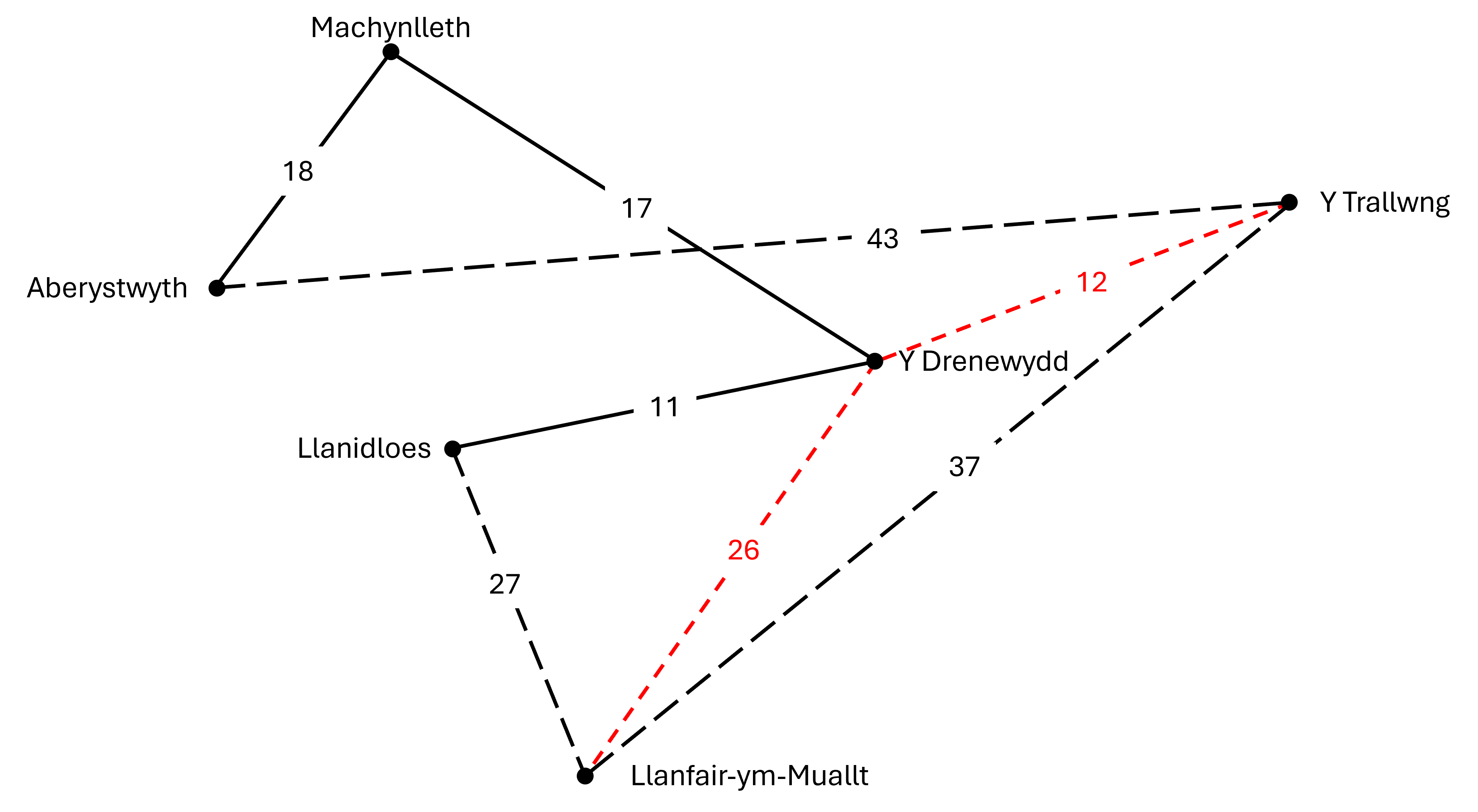
Y ddolen derfynol fyddai:
Aberystwyth → Machynlleth → Y Drenewydd → Llanidloes → Llanfair-ym-Muallt → Y Trallwng → Aberystwyth
Cyfanswm y pellter fyddai:
18 + 17 + 11 + 27 + 37 + 43 = 153
Llwybr 2:
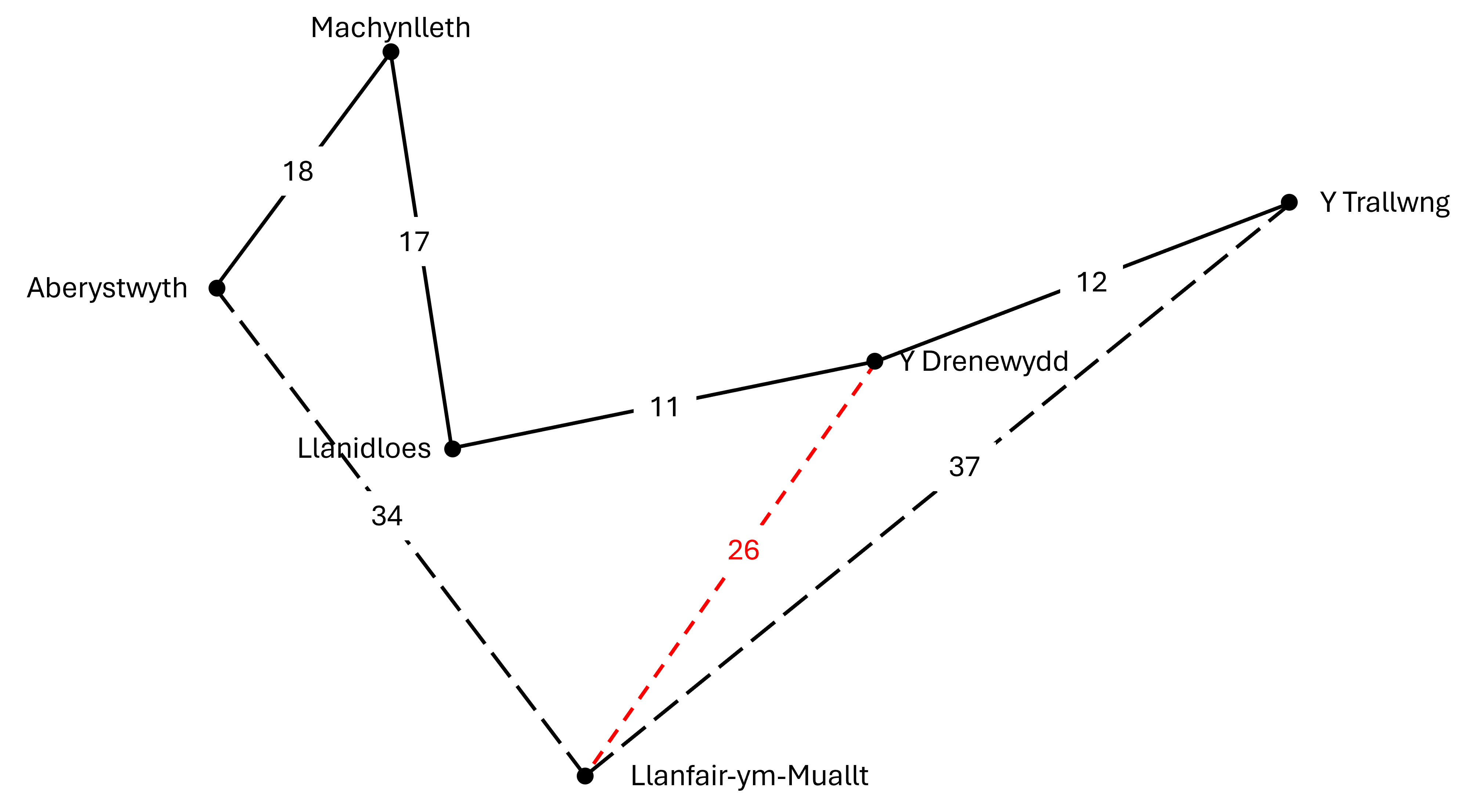
Y ddolen derfynol fyddai:
Aberystwyth → Machynlleth → Llanidloes → Y Drenewydd → Y Trallwng → Llanfair-ym-Muallt → Aberystwyth
Cyfanswm y pellter fyddai:
18 + 17 + 11 + 12 + 37 + 34 = 129
Mae hyn yn golygu mai Llwybr 2 sy'n creu'r llwybr byrraf i Siôn Corn fel y bydd yn gallu cwblhau'r her hon!